FiveThirtyEight has a new puzzle feature called The Riddler. This week they posted their second puzzle, which involves probability:
You arrive at the beautiful Three Geysers National Park. You read a placard explaining that the three eponymous geysers — creatively named A, B and C — erupt at intervals of precisely two hours, four hours and six hours, respectively. However, you just got there, so you have no idea how the three eruptions are staggered. Assuming they each started erupting at some independently random point in history, what are the probabilities that A, B and C, respectively, will be the first to erupt after your arrival?
Analytic solution
Responses were due last night at midnight, so I hope I’m not spoiling anything by sharing mine.
When you arrive at the park, the first eruption of geyser A is likely to occur at any time within the next two hours with a uniform probability. Denoting the number of hours until the first eruption of the geyser as “A”, A ~ Uniform(0, 2). Similarly, B ~ Uniform(0, 4) and C ~ Uniform(0, 6).
To compute the probability of geyser A erupting first, separately consider the cases where geysers B and C do and do not erupt within the first two hours of waiting.
Using Bayes Theorem:
$$Pr(A first \cap B<2, C<2) = Pr(A first | B < 2, C < 2) Pr(B < 2, C < 2)$$
Assuming independence of the geysers:
$$= Pr(A first | B < 2, C < 2) Pr(B < 2) Pr(C < 2)$$
Considering the case here, in which all three geysers erupt in the first two hours, the probability of any geyser erupting first is 1/3. The probability of geysers B and C erupting in the first two hours is easy to calculate.
$$= (1/3) \times (1/2) \times (1/3) = 1/18$$
Using similar logic:
$$Pr(A first \cap B > 2, C < 2) = (1/2) \times (1/2) \times (1/3) = 1/12$$ $$Pr(A first \cap B < 2, C > 2) = (1/2) \times (1/2) \times (2/3) = 1/6$$ $$Pr(A first \cap B > 2, C > 2) = 1 \times (1/2) \times (2/3) = 1/3$$
These disjoint events partition the sample space, so the law of total probability dictates:
$$Pr(A first) = 1/18 + 1/12 + 1/6 + 1/3 = 23/36 \approx 0.6389$$
Do the same thing to calculate the probability of geyser B erupting before the others:
$$Pr(B first \cap B < 2, C < 2) = (1/3) \times (1/2) \times (1/3) = 1/18$$ $$Pr(B first \cap B < 2, C > 2) = (1/2) \times (1/2) \times (2/3) = 1/6$$
Note that when geyser B does not erupt within the first two hours, another geyser is guaranteed to erupt before it:
$$Pr(B first \cap B > 2, C < 2) = 0$$ $$Pr(B first \cap B > 2, C > 2) = 0$$
Therefore:
$$Pr(B first) = 1/18 + 1/6 = 4/18 \approx 0.2222$$
And geyser C is similar:
$$Pr(C first \cap B < 2, C < 2) = (1/3) \times (1/2) \times (1/3) = 1/18$$ $$Pr(C first \cap B > 2, C < 2) = (1/2) \times (1/2) \times (1/3) = 1/12$$ $$Pr(C first) = 1/18 + 1/12 = 5/36 \approx 0.1389$$
Quick simulation
It never hurts to check results with a simulation. After all, math is hard and programming is easy.
library(dplyr)
library(ggplot2)
numSamples <- 1e6
# Generate random wait times for each geyser's next eruption
geysers <- data_frame(A = runif(numSamples, 0, 2),
B = runif(numSamples, 0, 4),
C = runif(numSamples, 0, 6))
geyserNames <- colnames(geysers)
# Identify the geyser with the smallest time-to eruption
geysers <- geysers %>%
mutate(first_geyser = geyserNames[max.col(-geysers[, geyserNames])])
# Plot the results
geysers %>%
ggplot(aes(x = first_geyser)) + geom_bar()
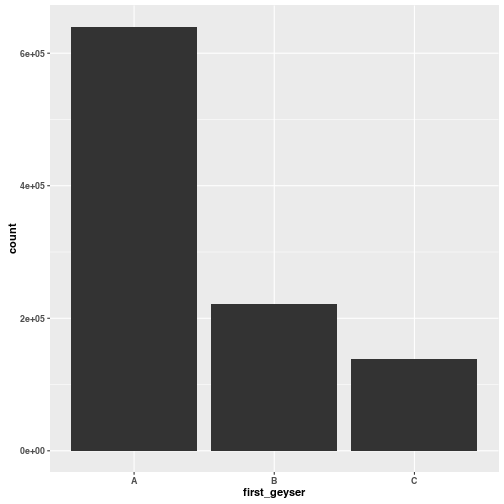
# Count observations and estimate probabilities
geysers %>%
count(first_geyser) %>%
mutate(prob_first = n / numSamples)
## Source: local data frame [3 x 3]
##
## first_geyser n prob_first
## 1 A 640093 0.640093
## 2 B 221439 0.221439
## 3 C 138468 0.138468
Close enough!