Introduction
How easy is it to change people’s minds about vaccinating their children? According to a recent study (Horne, Powell, Hummel & Holyoak, 2015), a simple intervention – which consisted of showing participants images, an anecdote, and some short warnings about diseases – made participants more likely to support childhood vaccinations. Here’s a good writeup of the article if you’re unable to read the original.
The authors placed their data online, which comprises pre- and post-intervention survey responses for three groups of participants:
- A control group
- An “autism correction” group that were shown evidence that vaccines don’t cause autism.
- A “disease risk” group that were shown images, an anecdote, and some short warnings about the diseases (such as rubella and measles) that the vaccines prevent.
I chose to look over this data for a couple reasons. First, I’m friends with two of the authors (University of Illinois Psychologists Zach Horne and John Hummel) and it’s good to see them doing cool work. Second, my own research has given me little opportunity to work with survey data, and I wanted more experience with the method. I was excited to try a Bayesian approach because it makes it possible to perform post hoc comparisons without inflating the “type I”" (false positive) error rates (see below).
Participants were given a surveys with five questions and asked to rate their level of agreement with each on a six-point scale.
| code | question |
|---|---|
| healthy | Vaccinating healthy children helps protect others by stopping the spread of disease. |
| diseases | Children do not need vaccines for diseases that are not common anymore. reverse coded |
| doctors | Doctors would not recommend vaccines if they were unsafe. |
| side_effects | The risk of side effects outweighs any protective benefits of vaccines. reverse coded |
| plan_to | I plan to vaccinate my children. |
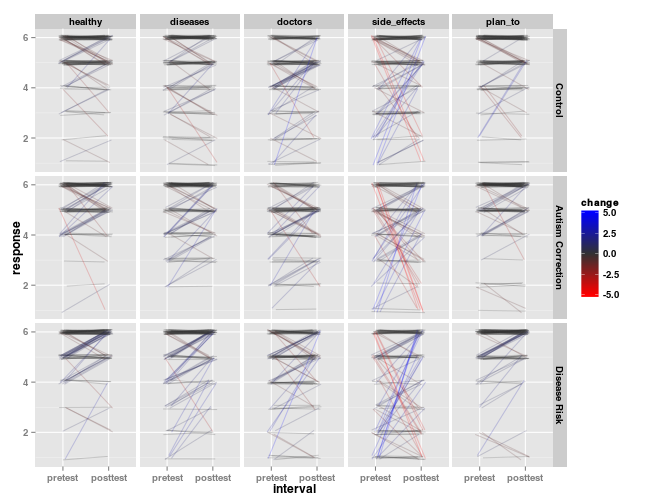
The above figure shows the data. Each line represents a single participant’s responses before and after the intervention, organized by intervention group and question. Lines are colored by the magnitude of the change in response; blue lines indicate an increase in agreement (toward a more pro-vaccine stance) and red lines indicate a reduction in agreement (a more anti-vaccine stance).
The JAGS code for the model is part of the source of this document, which is available through Git. It uses a Bayesian analog to a three-factor ANOVA, with a thresholded cummulative normal distribution serving as a link function. Such models fit ordinal responses (such as those obtained from surveys) well. The thresholds and variance of the link function were fit independently for each question. The mean of the function was estimated for each response using a linear combination of the levels of the question, the interval (pre-test vs. post-test), the intervention group, and all interactions between these factors.
Results
A “risk” intervention changes attitudes toward vaccination
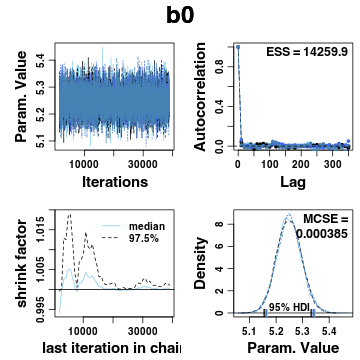
When fitting model parameters using Monte Carlo methods, it’s important to inspect the posterior distribution to make sure the samples converged. Here’s an example of one parameter, the intercept for the mean of the cummulative normal.
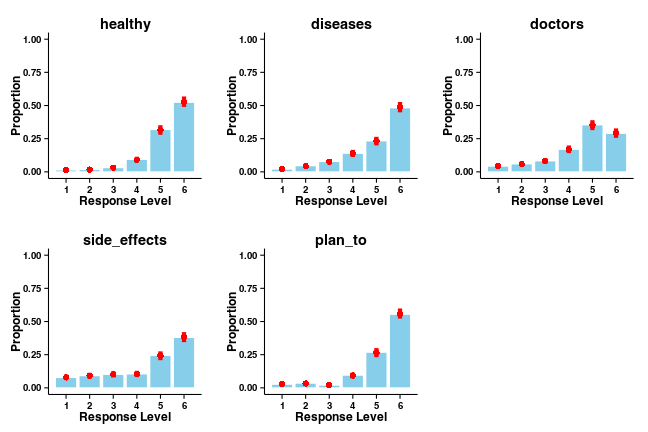
It’s also important to check the predictions made by a model against the data being fit, as “we cannot really interpret the parameters of the model very meaningfully when the model doesn’t describe the data very well”. Here are response histograms for each question, averaged across the levels of the other factors. Model predictions are superimposed on the histograms, along with the 95% HDI for each response.
Since the sampling procedure was well-behaved and the model describes the data well, we can use the parameter estimates to judge the size of the effects. Here are is the estimate of the change in attitude (post-test - pre-test) for each intervention group.
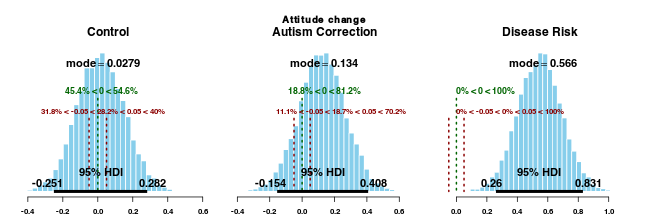
These plots highlight the 95% highest density interval (HDI) for the posterior distributions of the parameters. Also highlighted are a comparison value, which in this case is a pre- vs. post-test difference of 0, and a “range of practical equivalence” (ROPE) around the comparison value. The HDI of the posterior distribution of attitude shifts for the “disease risk” group" (but no other group) falls completely outside this ROPE, so we can reasonably conclude that this intervention changes participants’ attitudes toward vaccination.
We can also use the posterior distributions to directly estimate the shifts relative to the control group. Here is the difference between the attitude change observed for both the “autism correction” and “disease risk” groups compared to the attitude change in the control group.
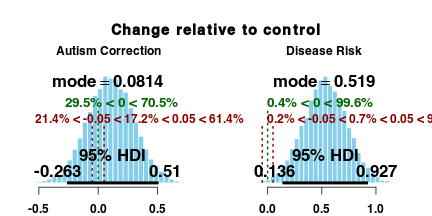
The posterior distribution above shows that “disease risk” participants shifted their response about half an interval relative to the control group following the intervention. The “autism correction” participants, however, did not show a credible change in vaccination attitudes. Bayesian estimation replicates the conclusions drawn by Horne and colleagues.
Post hoc comparisons
An analysis following the tradition of null-hypothesis significance testing (NHST) attempts to minimize the risk of “type I” errors, which occur when the “null” hypothesis (i.e., there is no effect) is erroneously rejected. The more tests performed in the course of an analysis, the more likely that such an error will occur due to random variation. The Wikipedia article on the “Multiple Comparisons Problem” is an approachable read on the topic and explains many of the corrections that are applied when making mulitple comparisons in a NHST framework.
Instead of focusing on type I error, the goal of Bayesian estimation is to estimate values of the parameters of a model of the data. The posterior distribution provides a range of credible values that these parameters can take. Inferences are made on the basis of these estimates; e.g., we see directly that the “disease risk” intervention shifts participants’ attitude toward vaccination about one half of an interval. Since a single model was fit to all the data, additional comparisons of parameter distributions don’t increase the chance of generating false positives. Gelman, Hill, and Yajima (2008) is a great resource on this.
For example, we can look at the size of the shift in attitude toward each question for each group. If we used an NHST approach, these 15 additional comparisons would either seriously inflate the type I error rate (using a p-value of 0.05 on each test would result in an overall error rate of 0.54), or require much smaller nominal p-values for each test.
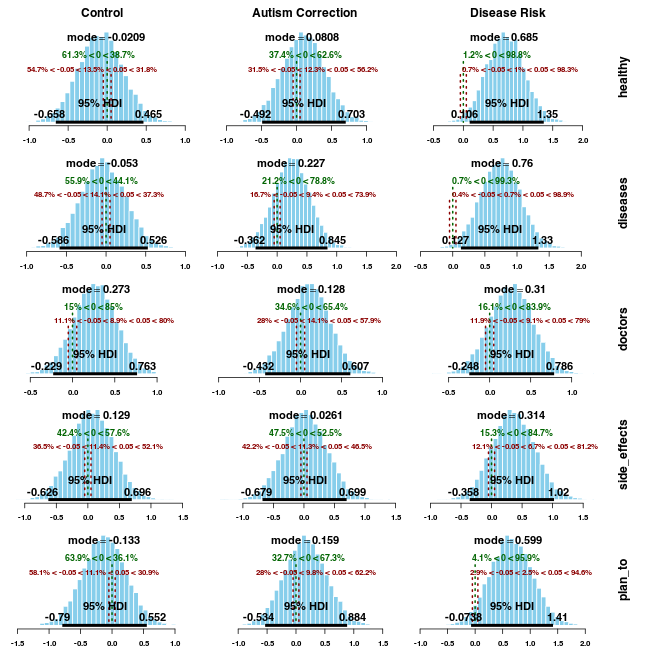
The only credible differences for single questions both occur for participants in the “disease risk” group. The “healthy” (“Vaccinating healthy children helps protect others by stopping the spread of disease.”) and “diseases” (“Children do not need vaccines for diseases that are not common anymore.”) questions show a reliable positive shift, which makes a lot of sense given the nature of the intervention. However, it’s important to note that the HDIs are very wide for these posteriors compared to the ones shown earlier. This is driven primarily by the fact that this comparison relies on a three-way interaction, which has greater variance (as is typical in traditional ANOVA models). The posterior mode of the change for the “plan_to” question (“I plan to vaccinate my children”) is fairly large for the “disease risk” group, but the wide HDI spans the ROPE around 0.
Expanding the models
My goal was to examine the conclusions made in the original report of these data. However, this is just one way to model the data, and different models are more appropriate for different questions. For instance, the standard deviation and thereshold values were fit separately for each question here, but these could instead be based on a hyperparameter that could iteself be modelled. I also excluded subject effects from the model; there were many subjects (over 300), so a full model with these included would take much longer to fit, but may produce more generalizable results. Bayesian estimation requires an investigator to be intentional about modelling decisions, which I consider to be an advantage of the method.
Prior probabilities
A defining characteristic of Bayesian analyses is that prior information about the model parameters is combined with their likelihood (derived from the data) to produce posterior distributions. In this analysis, I used priors that put weak constraints on the values of the parameters. If an investigator has reason to assume that parameters will take on certain values (e.g., the results of a previous study), this prior information can – and should – be incorporated into the analysis. Again, I like that these decisions have to be made deliberately.
Conclusions
Concerns about a possible link between childhood vaccination and autism is causing some parents to skip childhood vaccinations, which is dangerous (Calandrillo, 2004). However, an intervention that exposes people to the consequences of the diseases that vaccinations prevent makes them respond more favorably toward childhood vaccination. A separate group of participants did not change their attitudes after being shown information discrediting the vaccination-autism link, nor did a group of control participants.
Acknowledgements
Zach Horne made the data available for analysis (by anyone!), and gave useful feedback on an earlier version of this write-up. Much of the code for Bayesian estimation was cobbled together from programs distributed with Doing Bayesian Data Analysis (2nd ed) by John K. Kruschke.